[Reading Notes] Multimedia Systems — Algorithms, Standards and Industry Practices, Chapter 2 Digital Data Acquistion

[Reading Notes] Multimedia Systems — Algorithms, Standards and Industry Practices, Chapter 2 Digital Data Acquistion

1. Analog and Digital Signals

Analog: captured by recording devices, represented by a continuous function.

Digital: discrete set of values

Digital’s advantages over analog:

1. convinent for handling
2. Store without degradation(quality)
3. efficiently compress and transmit
4. easy to store

2. Analog to digital conversion

1. sampling
2. Quantization

digtial to analog: interpolation

2.1 Sampling

$x_s(n) = x(nT)$

T is the period, and 1/T is the frequency.

If T is too big, then it is artifact(error in signal processing)

Too small, need large amount of storage

In practical, sampling is always with filtering.

2.2 Quantization

It means how many bits to represent the number of samples.

$x_q(n) = Q[x_s(n)]$

Q is a rounding function that maps the continus value $x_s(n)$ to the nearest digital value using b bits.

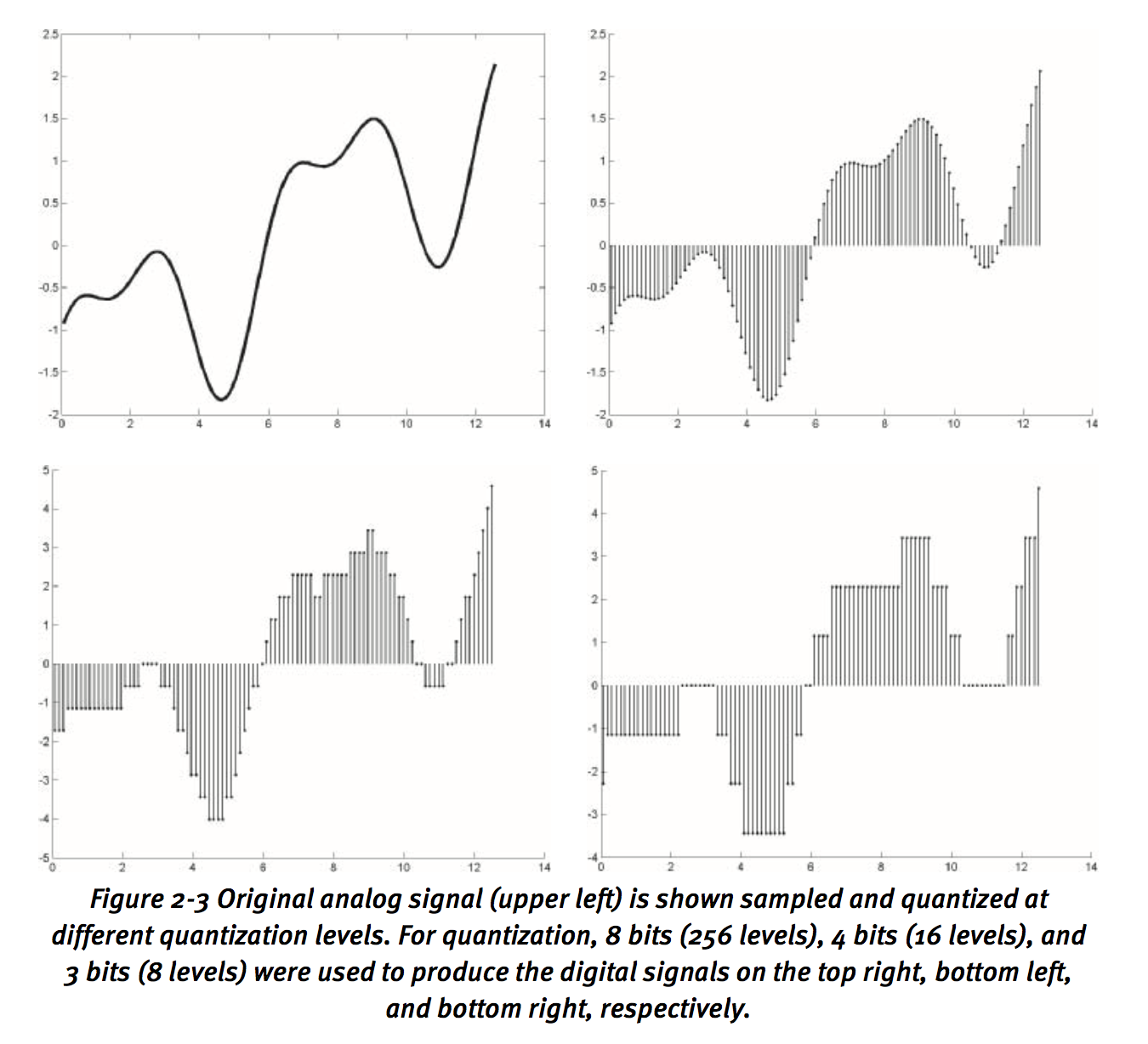
From the pic, diff bits could get diff precision.

Uniform quantization intervals vs Ununiform qunatization itervals

Sometimes, we want to give diff signals diff weights.

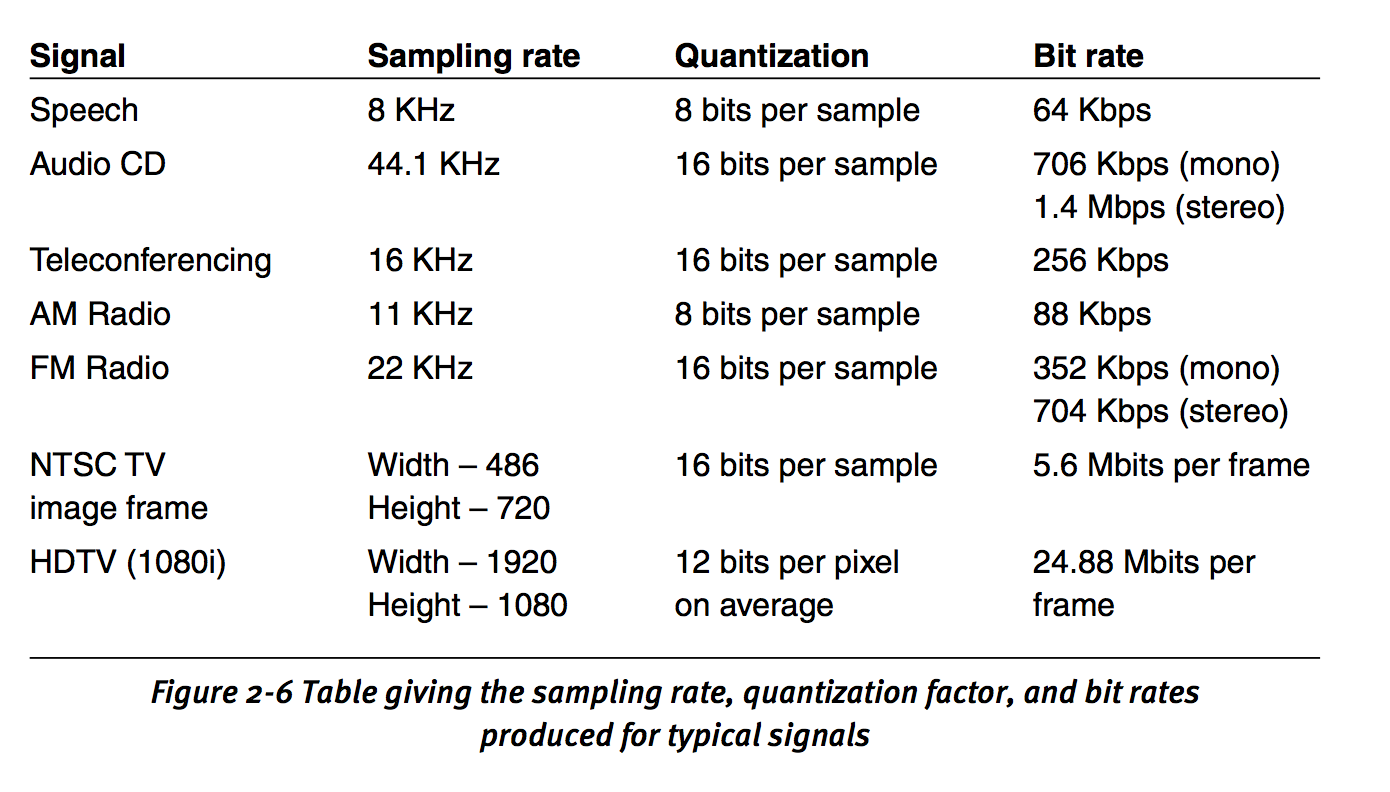
2.3 Bit Rate

Definition: number of bits being produced per second.
$$
Bit Rate = \cfrac{Bits}{Second}=(\cfrac{Samples\ produced}{Second}) * (\cfrac{Bits}{Sample}) \

=Sampling\ rate * Quantization\ bits\ per\ sample
$$

3. Signals and systems

3. 1 Linear Time Invariant Systems（LTI sys）

$$
If\ \ x(t) = c_1x_1(t) + c_2x_2(t) \
then\ \ y(t) = c_1y_1(t) + c_2y_2(t) \
where\ y_k(t)\ is\ the\ sole\ output\ resulting\ from\ x_k(t)
$$

Convolution of two signals f and g is mathematically represented by fg. It is the result of taking the integral of the first signal multiplied with the other signal reversed and shifted.
$$
\begin{aligned}
(fg) &= \int{-\infty}^{\infty} f(\tau) \cdot \ g(t-\tau)d\tau \
&= \int{-\infty}^{\infty} f(t-\tau) \cdot g(\tau)d\tau
\end{aligned}
$$

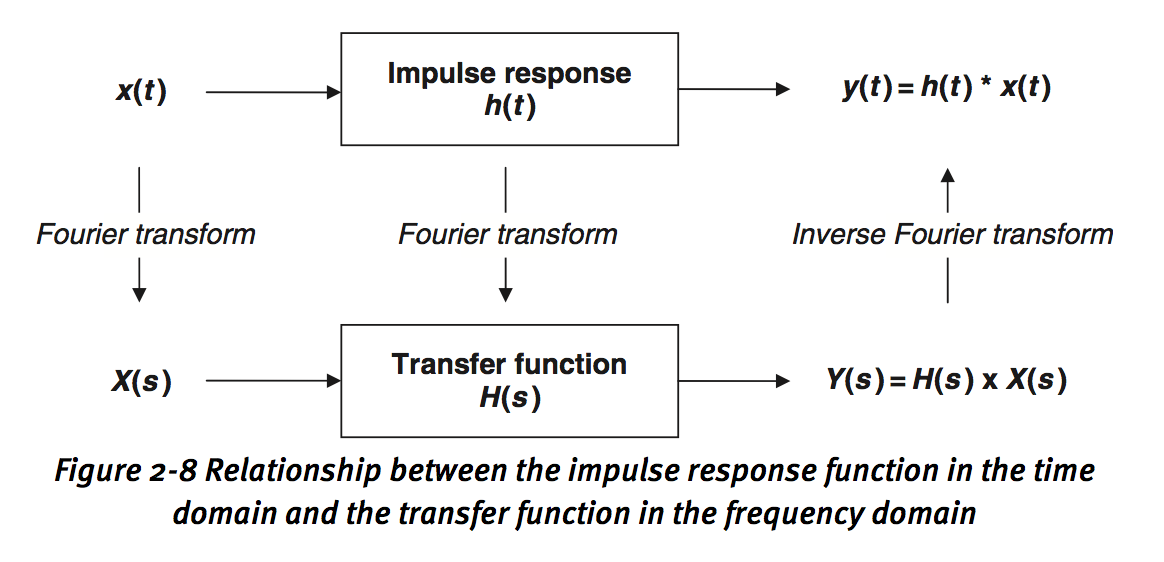
3.2 Fundamental Results in Linear Time Invariant Systems

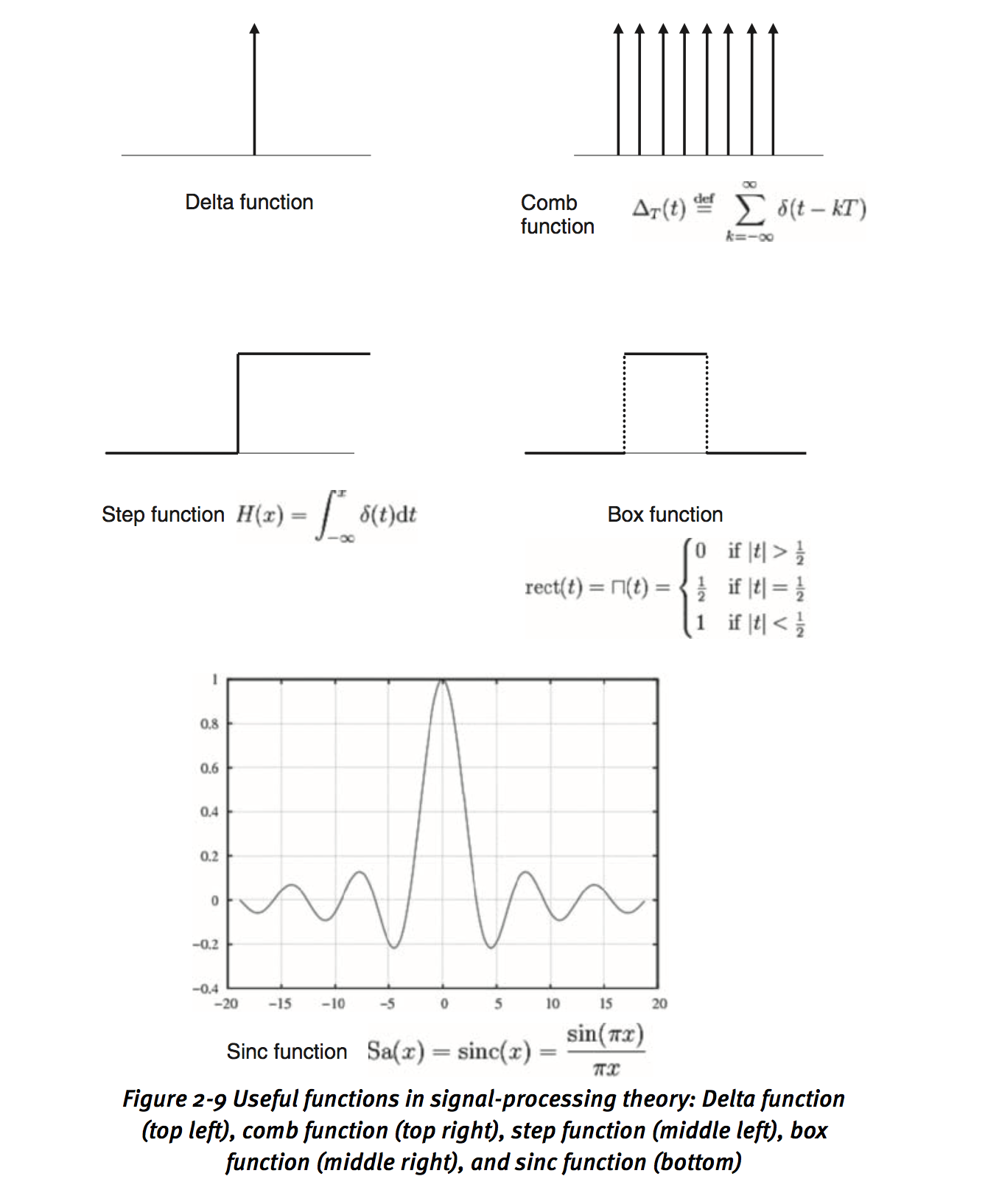
3.3 Useful Signals

Delta function, box function, step function.

3.4 The Fourier Transform

Every periodic, continus singal can be expressed as a weighted combination of sinusoid(sine and cosine) waves.

4 Sampling theorem and aliasing

The relation between signals and sampling rate: Nyquist theorem

The signal has to be sampled using a sampling frequency that is greater than twice the maximal frequency occuring in the signal.

If sampling freq is higher than Nyquist frequency? nothing special, it cannot reproduce the analog signal better.

What if lower? Cannot reproduce the original analog signal. Called aliasing.

Aliasing: loss of info during digitization.

4.1 Aliasing in Spatial Domains

cannot reconstruct or blur.

4.2 Aliasing in Temporal Domains

Wagon wheel effect This occurs because the movie camera has under sampled the wheels’ motion.

5 Filtering

1. Analog and 2. digital

e.g human voice: 4kHz sampling rate, use analog filter between microphone and recording device, then the resulting signal is then sampled at 8kHz.

5.1 Digital Filters

Analog filter: use analog electroic circuits made up from components such as resistors, capacitors, and operational amplifiers to produce the required filtering effect(in special range of freq).

Used in noise reduction, video signal enhancement, graphic equalizers in hi-fi systems.

Digital filter:

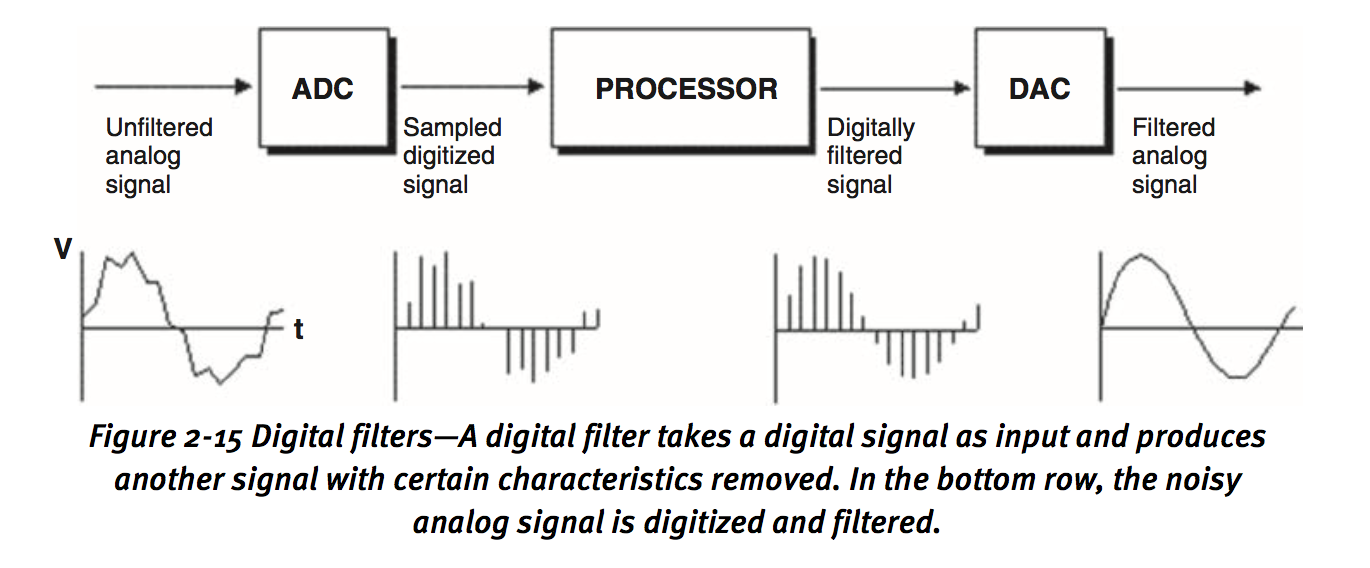
input and output for digital filter are both digital signals.

Advantages over analog filter:

1. Programmable, easy to change.
2. easy to design, test, and implement.
3. combined in parallel or cascaded in series.
4. stable
5. can handle low-frequency signals accurately. Also it could be applied in high-frequency signals in RF(radio frequency(used to be handled by analog filter))
6. Versatile. diff ways, diff types

Three categories:

Low-pass filter: remove high-freq, avoid aliasing artifacts while sampling.

Band-pass filter: only signals in defined band.

high-pass filter: remove low-freq, enhance edges and sharpen an image.

5.2 Filtering in 1D

…

5.3 Filtering in 2D

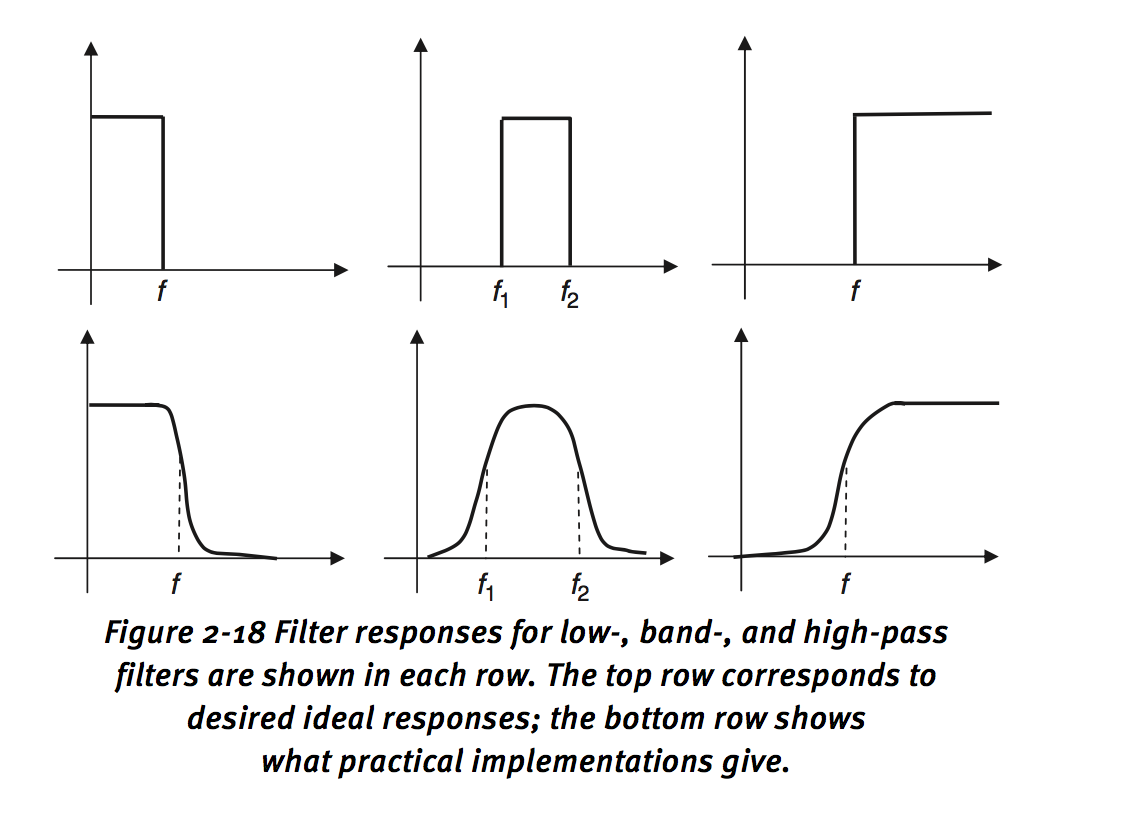
From the diff between ideal and practical filters: that’s the reason for which choose 44kHz, rather than exactly 40kHz sample rate. (human ear range 20Hz to 20kHz)

5.4 Subsampling

subsampling is a specific type of filter.

Subsampling an origianl signal by n: keep every $n^{th}$ sample and remove all the rest from the original singal. Consequnently, the size of data is also reduced by a factor of n.

Original m, after subsampling by n, then data size: m/n

subsampling might cause aliasing problem, prior to subsampling, low-pass digital filter could help to fix this problem.(why?)

6 Fourier Theory

A clear explanazation for FT(in Chinese): https://zhuanlan.zhihu.com/p/19763358
$$
f(t) = \sum_{i=0}^{i=\infty} Ai \times sin(i \omega t) + \sum{j=0}^{j=\infty} B_j \times cos(j \omega t)
$$