刷题中的一些经验总结

Posted on |

编程中的一些经验总结

  1. ！是整体取反，~是按位取反。

  2. ！的运算优先级大于%，因此有%操作的时候，最好直接上括号

  3. set 内部是无序的，因此distance操作对set来说没有意义。其内部是根据插入元素的大小进行排序的。

  4. lower_bound是返回第一个>= val的iterator, upper_bound则是返回第一个>val的iterator。所以lower_bound和upper_bound可能是相同的，如果数组里面正好没有这个值。

  5. 快慢指针如何实现：

    1. 1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      slow = head;
      fast = head->next; //注意这里的初始化操作，fast必须要初始化为head的next
      while(fast){
          fast = fast->next;
        	if(fast){
              slow = slow->next;
            	fast = fast->next;
          }
      }
      front = head;
      back = slow->next; // 必须是slow->next，而不能是slow,主要为了之后nullptr考虑
      slow->next = nullptr; // 只要slow->next=nullptr才能中断原始链表

    2. 这里的初始化，以及最后的赋值都是有讲究的，不是随意的。首先，初始化，slow初始化为head, fast初始化为head->next，这样的初始化与最后的赋值操作是配套的，back赋值为slow->next, front赋值为head, 然后slow->next=nullptr. 这样就可以将整个链断成俩半。

    3. 这样写的最主要的原因是，back只能赋值为slow->next，而不能赋值为slow. 这里简单说一下原因，详细的解释会在另一篇笔记中(c++的指针解密)详细阐述。首先明确，指针的值是表示指向的地址，比如node p = new node(1), 这里p这个变量的值就是1这个值在内存中的地址， 而&p这样的操作获取的值是指针自身的地址，换句话说是指针的指针值。因此我们常用的操作p=nullptr就是将p这个指针指向内存中一个特殊的区域，指向这个区域的指针代表其没有指向任何有意义的地方。之后用经常做的操作来进行表示，初始化`nodep; p=head这里p的值和head的值是***一致的***，但是&p!=&head这里意思是p和head是***俩个指针***，虽然他们都指向同一个地址。然后p->next == head->next以及&(p->next) == &(head->next)此时这俩个等式都是***成立的***，这意味着，p->next指向的值与head->next指向的值相同以及p->next与head->next是**同一个**指针。其中最为关键的地方就是p->next和head->next是**同一个指针！！！**~~当然这样有一个前提，node p;而不是nodep = new node(0)`。前面的初始化只是简单为p本身开辟了空间，而后面的初始化，则为p->val, p->next以及p本身都开辟了空间。这时候p->next就与head->next不是一个指针了，即使他们指向的内容相同。~~（经过实践，这里是错误的，实际上初始化方式不影响）。或者说编译器在编译的时候还是进行了一定的操作。

    4. 这样就能简洁优雅地操纵快慢指针了。

  6. Unsigned_int中暗藏杀机

    1
    2
    3
    4
    5
    6
    7
    8
    int n = 3;
    string s = "123";
    if(-1 >= s.size() - n){
        cout << "f**k" << endl;
    }
    ###结果是
    f**k

    这里为什么会输出呢？-1为什么就大于等于0了呢？是不是一脸懵逼中呢？

    原因就在于size()这个函数，这个函数返回值的类型是size_t, 也就是unsigned_int； 而当unsigned_int跟int做运算或者比较的时候，int都会默认转换成unsigned_int. 因此首先右边是size_t 0,然后-1与0比较的时候，-1转换成unsigned_int，则等于unsigned_MAX， 因此不等式为true.

  7. 如何通过一次循环删除vector中满足特定条件的所有items呢？

    1. 最傻瓜的想法

      1
      2
      3
      4
      5
      for(int i=0; i<v.size(); i++){
          if(condition){
      		v.erase(v.begin()+i);
          }
      }

      这样的操作实际上是行不通的，主要的原因是，erase操作的时候，会destroy掉对应的item然后剩余的元素会移动。所以v是会变动的。

    2. 那么正确的操作是什么呢

1
2
3
4
5
6
7
8
9
auto it = v.begin();
while(it!=v.end()){
    if(condition){
        it = v.erase(it);
    }
  	else{
        it++;
    }
}

这样的实现看起来不是很优雅，有没有优雅的方法呢？

1
2
// 利用remove_if操作来进行
v.erase(remove_if(v.begin(), v.end(), [](int i){i<3;}), v.end());

这个有一个专门的名字叫做erase-remove idiom

那么为什么同样是删除，这样的操作就可以呢？难道不改变vector的大小吗？事实上，主要的原因在于remove_if操作不是真正删除，而是将不满足条件的，将来不删除的放在vector的前面，而将所有满足条件的要删除的放置在vector后部，之后返回第一个要删除的元素的位置，然后erase直接就可以将这个位置到末尾所有的元素删除掉了。

这里还用到的一个知识点是，lambda函数，lambda我个人在Python里面用得多一些，平时刷题用C++的时候很少用到，同时GCC关于lambda函数似乎还有一个bug，可能需要在[]里面写上[this] 或者[&]才行编译通过。还有一个就是，如果里面的3是一个局部变量怎么办？ 这个时候也会有编译问题的，解决的方法就是[this, temp]将temp名字放到[]中，或者干脆把temp设置为全局变量也可以实现。

​

不常见的一些算法和数据结构

  1. Morris Algorithm 该算法可以以O(1)的空间，O(N)的时间复杂度来对树进行中序遍历，当然也可以推广到前序和后序。利用了线索二叉树的性质。Thread binary tree.

  2. Kadane’s algorithm

    1. 该算法用来在一列正负数中找到和最大的序列。

    2. 1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      Initialize:
          max_so_far = 0
          max_ending_here = 0
      Loop for each element of the array
        (a) max_ending_here = max_ending_here + a[i]
        (b) if(max_ending_here < 0)
                  max_ending_here = 0
        (c) if(max_so_far < max_ending_here)
                  max_so_far = max_ending_here
      return max_so_far

    3. 算法的思想比较简单，就是比较当前的大小，如果是负，那么意味着可以舍弃前面的和。在遍历的同时更新一个全局最大值。

  1. Binary Indexed Tree(Fenwich Tree)
    1. time complexity: query and modification O(logn)
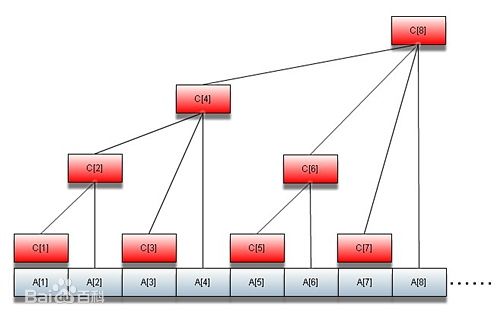
    2. binaryindexedtree
    3. 所有的奇数位置的数字和原数组对应位置的相同，偶数位置是原数组若干位置之和
    4. 如何确定某个位置到底是几个数组成，根据坐标的最低位Low Bit来决定
    5. 最低位的计算方法有俩种： x&(x^(x-1)) 或者是x&-x
    6. 这里的结构index必须从1开始，而不能从0开始，因为0&-0还是0，并没有更新index, 像1&-1=1, 2&-2=2, 4&-4=4, 也就是说C2, C4, C8都包含A1. (j+=j&-j, 1+1=2, 2+2=4, 4+4=8)